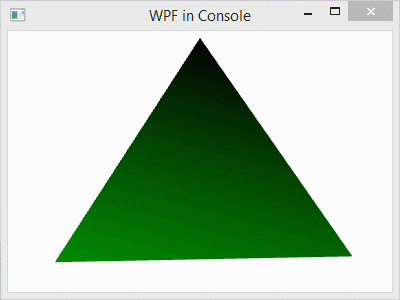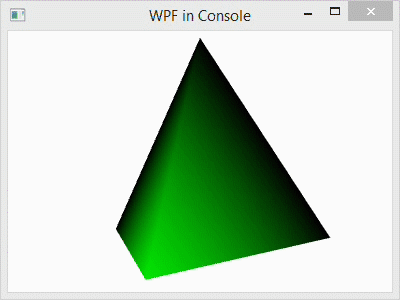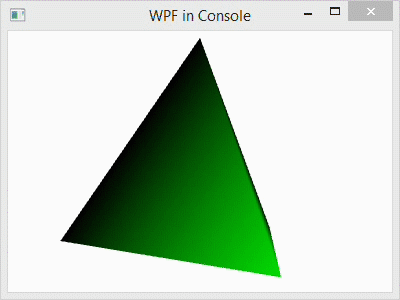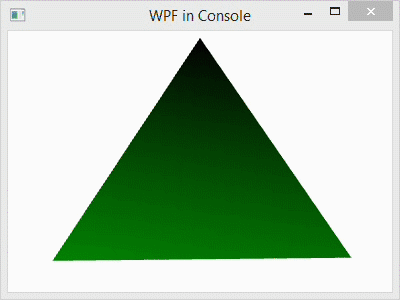
In this post, I explain the basic Windows Presentation Foundation programming elements of a 3D scene in C#. The C# code that I use for demonstration creates a simple tetrahedron model and rotates it around the vertical axis.
To create the project, follow these steps:
- Begin with the project from our prior blog post, or create a new WPF project.
- Add a class file to the project: left-click PROJECT in the menubar and left-click Add Class… in the submenu.
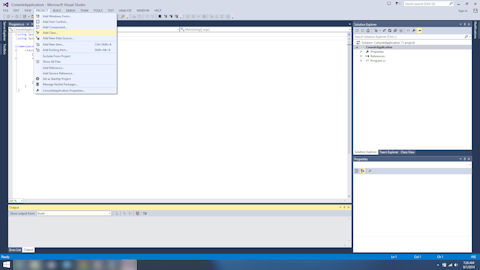
- This pops up the Add New Item dialog. Select Installed->Visual C# Items in the left-hand pane.

- Then left-click Class in the center pane to select it.
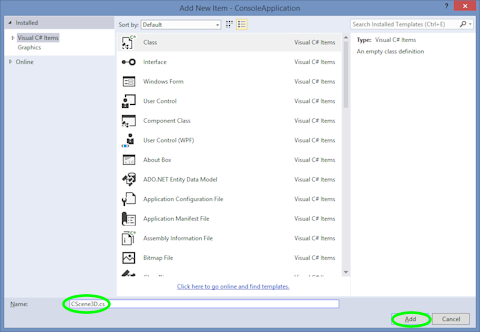
- Finally, rename the class by left-clicking the text box next to Name: at the bottom of the window and entering CScene3d.cs. Finish adding the class by left-clicking the Add button.
- Next, copy the code for “CScene3D.cs” below into the file of the same name in your project.
- Finally, finish the code by adding this line to “Program.cs” as shown in the code below to allow the window to display the 3D scene:
qWindow.Content = TestScenes.Test5();
- Compile and execute the program by left-clicking DEBUG in the menubar and left-clicking Start Without Debugging in the submenu. After a few seconds, the code will be compiled and a window will pop up displaying a rotating tetrahedron.
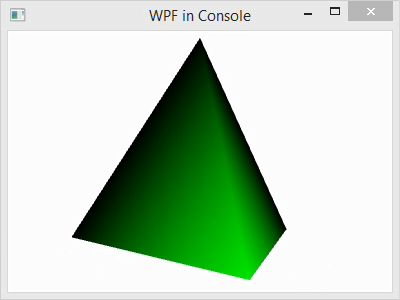
The WPF scene creation in “CScene3D.cs” consists of a few basic steps, which can be outlined as follows:
- Create a camera and add it.
- Create a lighting model and add it.
- Create a geometric model and add it
- Create points, triangles, and normals
- Set the material properties
- Create and apply transforms
For simplicity, I have skipped some steps, like adding normals, and accepted default values for much of the rest. At the end, I have collected components to added them appropriately. Pay close attention to that.
Program.cs
using System;
using System.Windows;
namespace ConsoleApplication {
class Program {
[STAThread]
static void Main(string[] args) {
Window qWindow = new Window();
qWindow.Title = "WPF in Console";
qWindow.Width = 400;
qWindow.Height = 300;
qWindow.Content = CScene3D.Test();
qWindow.ShowDialog();
}
}
}
CScene3D.cs
using System;
using System.Windows;
using System.Windows.Controls;
using System.Windows.Media;
using System.Windows.Media.Media3D;
using System.Windows.Media.Animation;
namespace ConsoleApplication {
class CScene3D {
// Animation - Tetrahedron (upright, looking slightly up from below)
public static Viewport3D Test() {
// Define the camera
PerspectiveCamera myPCamera = new PerspectiveCamera();
myPCamera.Position = new Point3D(0, .2, 3);
// Define a lighting model
DirectionalLight myDirectionalLight = new DirectionalLight();
// Define the geometry
const double kdSqrt2 = 1.4142135623730950488016887242097;
const double kdSqrt6 = 2.4494897427831780981972840747059;
// Create a collection of vertex positions
Point3DCollection myPositionCollection = new Point3DCollection();
myPositionCollection.Add(new Point3D(0.0, 1.0, 0.0));
myPositionCollection.Add(new Point3D(2.0 * kdSqrt2 / 3.0, -1.0 / 3.0, 0.0));
myPositionCollection.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, kdSqrt6 / 3.0));
myPositionCollection.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, -kdSqrt6 / 3.0));
// Create a collection of triangle indices
Int32Collection myTriangleIndicesCollection = new Int32Collection();
// Triangle
myTriangleIndicesCollection.Add(0);
myTriangleIndicesCollection.Add(2);
myTriangleIndicesCollection.Add(1);
// Triangle
myTriangleIndicesCollection.Add(0);
myTriangleIndicesCollection.Add(1);
myTriangleIndicesCollection.Add(3);
// Triangle
myTriangleIndicesCollection.Add(0);
myTriangleIndicesCollection.Add(3);
myTriangleIndicesCollection.Add(2);
// Triangle
myTriangleIndicesCollection.Add(1);
myTriangleIndicesCollection.Add(2);
myTriangleIndicesCollection.Add(3);
MeshGeometry3D myMeshGeometry3D = new MeshGeometry3D();
myMeshGeometry3D.Positions = myPositionCollection;
myMeshGeometry3D.TriangleIndices = myTriangleIndicesCollection;
// Apply the mesh to the geometry model.
GeometryModel3D myGeometryModel = new GeometryModel3D();
myGeometryModel.Geometry = myMeshGeometry3D;
// Define the material for the geometry
SolidColorBrush qColorBrush = new SolidColorBrush(Color.FromArgb(255, 0, 255, 0));
DiffuseMaterial myMaterial = new DiffuseMaterial(qColorBrush);
myGeometryModel.Material = myMaterial;
// Define the transformation, if any. In this case, we use an animated transformation
RotateTransform3D myRotateTransform =
new RotateTransform3D(new AxisAngleRotation3D(new Vector3D(0, 1, 0), 1));
DoubleAnimation myAnimation = new DoubleAnimation();
myAnimation.From = 1;
myAnimation.To = 361;
myAnimation.Duration = new Duration(TimeSpan.FromMilliseconds(5000));
myAnimation.RepeatBehavior = RepeatBehavior.Forever;
myRotateTransform.Rotation.BeginAnimation(AxisAngleRotation3D.AngleProperty, myAnimation);
myGeometryModel.Transform = myRotateTransform;
// Collect the components
Model3DGroup myModel3DGroup = new Model3DGroup();
myModel3DGroup.Children.Add(myDirectionalLight);
myModel3DGroup.Children.Add(myGeometryModel);
ModelVisual3D myModelVisual3D = new ModelVisual3D();
myModelVisual3D.Content = myModel3DGroup;
Viewport3D myViewport3D = new Viewport3D();
myViewport3D.Children.Add(myModelVisual3D);
myViewport3D.Camera = myPCamera;
return myViewport3D;
}
}
}

 RSS
RSS Atom
Atom Feedburner
Feedburner