The normal vectors that are used to calculate the light reflections for 3D graphics in Window Presentation Foundation are based on how the mesh geometry is specified. Of course, the normals (normal vectors) can be set manually, but when they are calculated automatically for vertices, the normals are formed by averaging the normals of the adjacent triangles as specified by the geometry graph. To illustrate, I have a tetrahedron with two different graph specifications, but the same vertices.
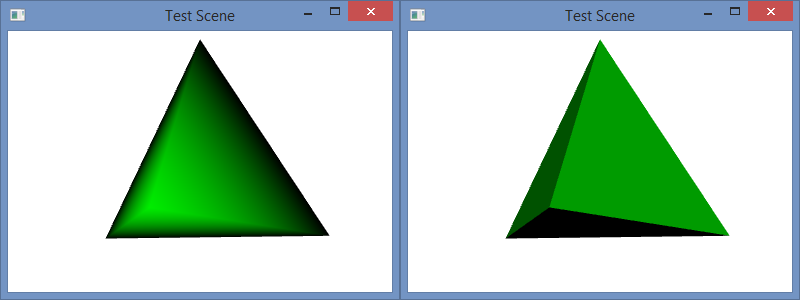
The C# project for this blog post is the same as it was in my prior blog post, and the code is similar as well. In that post, I used normals that were calculated as the average of the three adjacent triangle faces, and the color was smoothly interpolated across each face. In this post, I have changed the camera angle slightly, but I have used the same normal calculation in the code below. However, I have also include code for flat shading as well as the code for smooth shading for comparison. You can copy and paste the flat shading code over the smooth shading to try it out. A side-by-side comparison of the two is shown in the image below: left is smooth and right is flat.
The code snippets below are comprised of the code for the two geometry specifications and our two code files: Program.cs and CScene3D.cs. Each geometry specifications can be pasted into the file CScene3D.cs over the other to replace it to set the shading accordingly. In the flat shading model, each vertex is specified three times: once for each of the triangle faces that contains it. In the smooth mode, each vertex is shared by three triangle faces; note the vertex indices for each triangle.
This explains how the normal calculations are made for each vertex. They are averaged over all of the triangles that contain the vertex. Since each vertex in the flat model is contained in exactly one triangle, the shading is specified by that single face–like the rest of the vertices in that triangle. That is why the shading is constant over each face.
To understand why either these models might be used, consider the purpose of the rendering. For a facetted surface, like a diamond, we would want to use the flat shading model to correctly illustrate the facets. For a smooth surface, like the Earth, we would want to use a smooth model to hide the polygons and make the surface appear smoother. In this program, we would probably want to used flat shading because the model is a tetrahedron. A tetrahedron is facetted, and it’s corners are so sharp that they can never appear smooth. So, smooth shading always looks strange for it.
Flat Model
// Create a collection of vertex positions
Point3DCollection qPoints = new Point3DCollection();
// Triangle 1
qPoints.Add(new Point3D(0.0, 1.0, 0.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, kdSqrt6 / 3.0));
qPoints.Add(new Point3D(2.0 * kdSqrt2 / 3.0, -1.0 / 3.0, 0.0));
// Triangle 2
qPoints.Add(new Point3D(0.0, 1.0, 0.0));
qPoints.Add(new Point3D(2.0 * kdSqrt2 / 3.0, -1.0 / 3.0, 0.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, -kdSqrt6 / 3.0));
// Triangle 3
qPoints.Add(new Point3D(0.0, 1.0, 0.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, -kdSqrt6 / 3.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, kdSqrt6 / 3.0));
// Triangle 4
qPoints.Add(new Point3D(2.0 * kdSqrt2 / 3.0, -1.0 / 3.0, 0.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, kdSqrt6 / 3.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, -kdSqrt6 / 3.0));
// Designate Triangles
Int32Collection qTriangles = new Int32Collection();
// Triangle 1
qTriangles.Add(0);
qTriangles.Add(1);
qTriangles.Add(2);
// Triangle 2
qTriangles.Add(3);
qTriangles.Add(4);
qTriangles.Add(5);
// Triangle 3
qTriangles.Add(6);
qTriangles.Add(7);
qTriangles.Add(8);
// Triangle 4
qTriangles.Add(9);
qTriangles.Add(10);
qTriangles.Add(11);
Smooth Model
// Create a collection of vertex positions
Point3DCollection qPoints = new Point3DCollection();
qPoints.Add(new Point3D(0.0, 1.0, 0.0));
qPoints.Add(new Point3D(2.0 * kdSqrt2 / 3.0, -1.0 / 3.0, 0.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, kdSqrt6 / 3.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, -kdSqrt6 / 3.0));
// Designate Triangles
Int32Collection qTriangles = new Int32Collection();
// Triangle 1
qTriangles.Add(0);
qTriangles.Add(2);
qTriangles.Add(1);
// Triangle 2
qTriangles.Add(0);
qTriangles.Add(1);
qTriangles.Add(3);
// Triangle 3
qTriangles.Add(0);
qTriangles.Add(3);
qTriangles.Add(2);
// Triangle 4
qTriangles.Add(1);
qTriangles.Add(2);
qTriangles.Add(3);
Program.cs
using System;
using System.Windows;
namespace ConsoleApplication {
class Program {
[STAThread]
static void Main(string[] args) {
Window qWindow = new Window();
qWindow.Title = "WPF in Console";
qWindow.Width = 400;
qWindow.Height = 300;
qWindow.Content = CScene3D.Test();
qWindow.ShowDialog();
}
}
}
CScene3D.cs
using System;
using System.Windows;
using System.Windows.Controls;
using System.Windows.Media;
using System.Windows.Media.Media3D;
using System.Windows.Media.Animation;
namespace ConsoleApplication {
class CScene3D {
// Animation - Tetrahedron (upright, looking slightly up from below)
public static Viewport3D Test() {
// Define the camera
PerspectiveCamera qCamera = new PerspectiveCamera();
qCamera.Position = new Point3D(0, -.5, 2);
qCamera.LookDirection = new Vector3D(0, .3, -1);
qCamera.UpDirection = new Vector3D(0, 1, 0);
qCamera.FieldOfView = 60;
// Define a lighting model
DirectionalLight qLight = new DirectionalLight();
// Define the geometry
const double kdSqrt2 = 1.4142135623730950488016887242097;
const double kdSqrt6 = 2.4494897427831780981972840747059;
// Create a collection of vertex positions
Point3DCollection qPoints = new Point3DCollection();
qPoints.Add(new Point3D(0.0, 1.0, 0.0));
qPoints.Add(new Point3D(2.0 * kdSqrt2 / 3.0, -1.0 / 3.0, 0.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, kdSqrt6 / 3.0));
qPoints.Add(new Point3D(-kdSqrt2 / 3.0, -1.0 / 3.0, -kdSqrt6 / 3.0));
// Designate Triangles
Int32Collection qTriangles = new Int32Collection();
// Triangle 1
qTriangles.Add(0);
qTriangles.Add(2);
qTriangles.Add(1);
// Triangle 2
qTriangles.Add(0);
qTriangles.Add(1);
qTriangles.Add(3);
// Triangle 3
qTriangles.Add(0);
qTriangles.Add(3);
qTriangles.Add(2);
// Triangle 4
qTriangles.Add(1);
qTriangles.Add(2);
qTriangles.Add(3);
MeshGeometry3D qMesh = new MeshGeometry3D();
qMesh.Positions = qPoints;
qMesh.TriangleIndices = qTriangles;
// Apply the mesh to the geometry model.
GeometryModel3D myGeometryModel = new GeometryModel3D();
myGeometryModel.Geometry = qMesh;
// Define the material for the geometry
SolidColorBrush qBrush = new SolidColorBrush(Color.FromArgb(255, 0, 255, 0));
DiffuseMaterial qMaterial = new DiffuseMaterial(qBrush);
myGeometryModel.Material = qMaterial;
// Define the transformation, if any. In this case, we use an animated transformation
RotateTransform3D qRotation =
new RotateTransform3D(new AxisAngleRotation3D(new Vector3D(0, 1, 0), 1));
DoubleAnimation qAnimation = new DoubleAnimation();
qAnimation.From = 1;
qAnimation.To = 361;
qAnimation.Duration = new Duration(TimeSpan.FromMilliseconds(5000));
qAnimation.RepeatBehavior = RepeatBehavior.Forever;
qRotation.Rotation.BeginAnimation(AxisAngleRotation3D.AngleProperty, qAnimation);
myGeometryModel.Transform = qRotation;
// Collect the components
Model3DGroup qModelGroup = new Model3DGroup();
qModelGroup.Children.Add(qLight);
qModelGroup.Children.Add(myGeometryModel);
ModelVisual3D qVisual = new ModelVisual3D();
qVisual.Content = qModelGroup;
Viewport3D qViewport = new Viewport3D();
qViewport.Children.Add(qVisual);
qViewport.Camera = qCamera;
return qViewport;
}
}
}
Tags: 3d, C Sharp, C#, flat shading, interpolated, lighting, nomal vector, normals, polygon, smooth shading, tetrahedron, windows presentation foundation, wpf
Michael HallBy: Michael Hall

 RSS
RSS Atom
Atom Feedburner
Feedburner