In this algorithms lesson video, we explained what a comparsion sort is and how to make a fully optimized version of a comparison sort. We started by explaning what a comparison is. Next, we demonstrated how to run an optimized comparison search on a sorted array and reported its time complexity as O(log(n)), where the size of the array in n. Then we explained that number of possible arrangements of the elements of an array is n! for an array of size n. This led us, by an analogy to our search, to the fact that the fastest sorting algorithm must use at least the ceiling of the log base 2 of n! steps, for an array of size n. We showed that this optimal sort would not improve the time complexity over the other O(n*log(n)) algorithms, even though it would reduce the number of steps required. Finally, we demonstrated the implementation of an ideally optimized comparison sort for an array of size 4.

What is a comparison?

A comparison is an operation that compares two elements and returns a boolean value to indicate whether the relationship between the two elements holds. The common comparison operations that we typically use for sorting are less than (<) and greater than (>). For our purposes, we will use a comparison to divide a set into two parts, based on whether or not the elements of the set satisfy the comparison relationship.

Optimized Comparison Searching

In the video, we demonstrate how to search an array in the shortest possible time. Essentially, we compare the entry that we are searching for to the middle of the remaining entries to eliminate half of the possible locations at each comparison. This gives us the location of the entry in the ceiling of the log of n comparisons, which is the same as the O(log(n)).

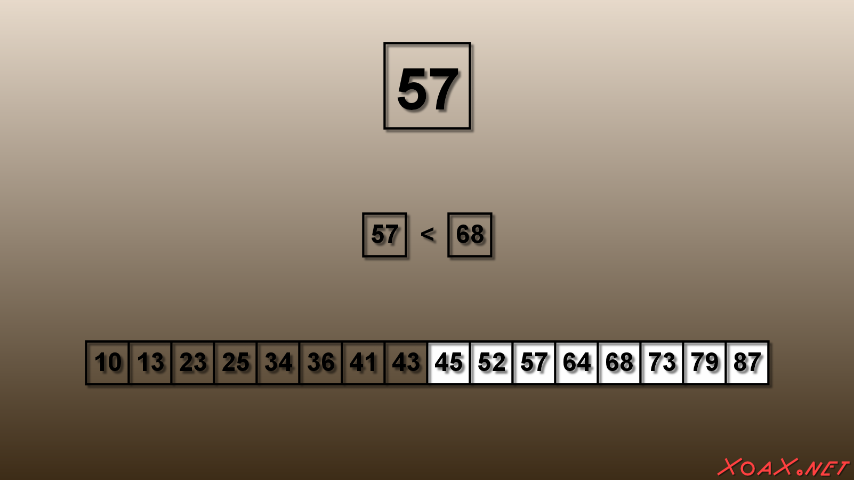
Optimized Comparison Sort

With n entries in an array, there are n! ways to arrange them--one of which is sorted. With n! possibilities, we can theorectically eliminate half of them at each comparison on two elements. Unlike searching, it is not obvious that we can actually achieve the goal of elminating half of the arrangements at each search. However, if we can, we can sort an array in the ceiling of log of n! comparisons. Although this seems better than n times the log of n, the two are equivalent in time complexity terms of time complexity. This can be demonstrated by showing that the ceiling of log(n!) is in big Omega of n*log(n). All of the logs are base 2.

Explanation of the Calculations

1. By the definition of the ceiling function, ⌈x⌉ ≥ x
2. Log of a product is the sum of the logs: log(ab) = log(a) + log(b)
3. Truncation of a nonnegative sum: a + b ≥ a, where b ≥ 0
4. Collect terms. Extra term for n even
5. Log of a division is the difference of the logs: log(a/b) = log(a) - log(b)
6. Log of 2 is 1 because the base is 2
7. Distributive Proterty: x(a + b) = xa + xb
8. (n/2)log(n) = (n/4)log(n) + (n/4)log(n)
9. ((n/4)log(n) - n/2) ≥ 0 for n ≥ 4

Big Omega

This demonstrate that the ceiling of the log of n! is in big omega of n*log(n). The constants c = 1/4 and n0 = 4 satisfy the definition of the big omega.

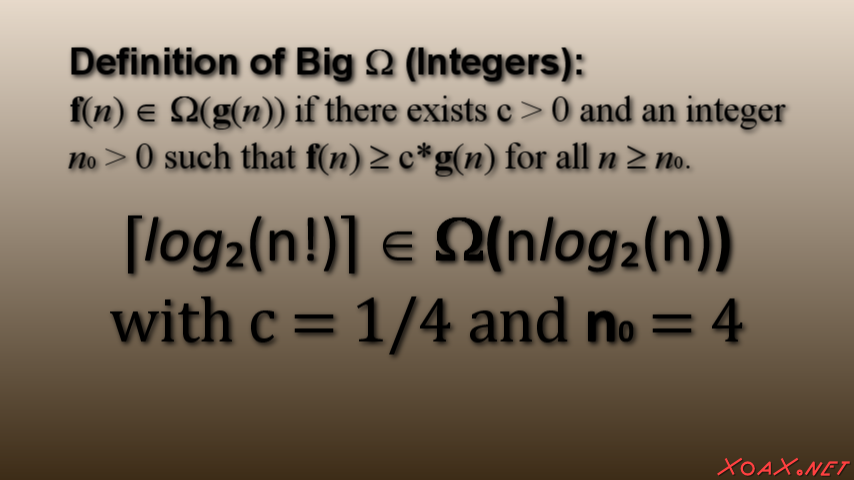
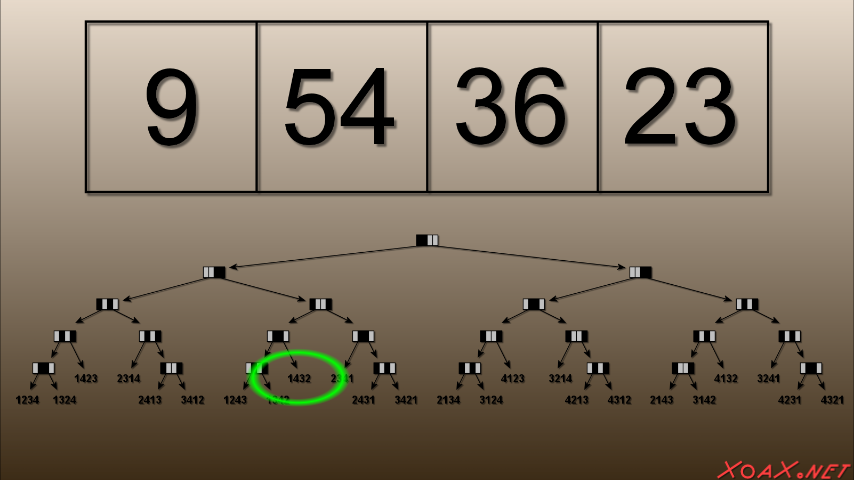
Optimal Comparison Sort for n = 4

Below, we have a decision tree that can be used to sort an array of size 4. Each node tells us which two elements are to be compared in black. If the less than relationship holds for the two elements, we move to the left child node. If it does not, then we move to the right child node. We continue this process until we reach a leaaf node that tells us to which permutation the array corresponds. Once we find the permutation, we can sort the array by applying the inverse permutation.

For illustration, we begin with the array shown: [9, 54, 36, 23]. At the root node, we compare the first two entries to see whether (9 < 54) is true. Since it is true, we move to the left child and compare the last two entries to determine if (36 < 23) is true. Since it is not, we move to the right child and compare the first and last entreis to see whether (9 < 23) is true. Since it is, we move to the left node and compare the middle entries to see whether (54 < 36) is true. Since it is not true, we move to the right node which is a leaf containing the permutation [1,4,3,2]. To sort the array, we apply the inverse permutation, which is itself ([1,4,3,2]), to swap the second and fourth entries.